sucesion

05.03.2014 12:37

Encontrando el N-ésimo TérminoCuando se habla del N-ésimo Término de una sucesión nos referimos a la regla o fórmula que rige el patrón que siguen todos los elementos de la misma. Para encontrar esta formula debemos seguir los siguientes pasos:

Encontrando el N-ésimo Término
1. Determinar el valor de a(1). Es el primer término de la sucesión.

2. Encontrar el cociente d entre dos términos consecutivos en la sucesión, ese cociente d debe ser igual para cualquier par de términos escogidos.

3. Comprobar el resultado dado, haciendo la respectiva sucesión paso a paso.
Si no tenemos una sucesión, entonces utilizar la fórmula cuando tenemos un término y el cociente o constante entre dos términos.

la fórmula para el término general de una sucesión geométrica es:

$a$ n = a 1 · r n - 1

Finita o infinita

Si la sucesión sigue para siempre, es una sucesión infinita,

si no es una sucesión finita

Ejemplos

{1, 2, 3, 4 ,...} es una sucesión muy simple (y es una sucesión infinita)

{20, 25, 30, 35, ...} también es una sucesión infinita

{1, 3, 5, 7} es la sucesión de los 4 primeros números impares (y es una sucesión infinita)

{4, 3, 2, 1} va de 4 a 1 hacia atrás

{1, 2, 4, 8, 16, 32, ...} es una sucesión infinita donde vamos doblando cada término

{a, b, c, d, e} es la sucesión de las 5 primeras letras en order alfabético

{a, l, f, r, e, d, o} es la sucesión de las letras en el nombre "alfredo"

{0, 1, 0, 1, 0, 1, ...} es la sucesión que alterna 0s y 1s (sí, siguen un orden, en este caso un orden alternativo)

En orden

Cuando decimos que los términos están "en orden", ¡nosotros somos los que decimos qué orden! Podría ser adelante, atrás... o alternando... ¡o el que quieras!

Una sucesión es muy parecida a un conjunto, pero con los términos en orden (y el mismo valor sí puede aparecer muchas veces).

Ejemplo: {0, 1, 0, 1, 0, 1, ...} es la sucesión que alterna 0s y 1s. El conjunto sería sólo {0,1}

La regla

Una sucesión sigue una regla que te dice cómo calcular el valor de cada término.

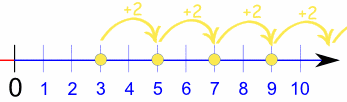
Ejemplo: la sucesión {3, 5, 7, 9, ...} empieza por 3 y salta 2 cada vez:

Interpolación de términos en una progresión geométrica

Interpolar medios geométricos o proporcionales entre dos números, es construir una progresión geométrica que tenga por extremos los números dados.

Sean los extremos a y b, y el número de medios a interpolar m.