sucesión matematica

04.03.2014 00:00

sucesion matematica

bueno muchachos hoy vamos a hablar de la sucesion matematica.

¿que es?

una sucesion matematica es un conjunto ordenado de objetos matematicos generalmente numeros. Cada uno de ellos es denominado termino (tambien elemento o miembro) de la sucesion y al numero de elementos ordenados (posiblemente infinitos) se le denomina la longitud de la sucesion. No debe confundirse con una serie matematica, que es la suma de los terminos de una sucesion.

ejemplo:

La sucesion (A,B,C) es una sucesion de letras que difiere de la sucesion (C,A,B). En este caso se habla de sucesiones finitas (de longitud igual a 3). Un ejemplo de sucesion infinita seria de numeros positivos pares: 2,4,6,8, .....

En ocaciones se identifica a las sucesiones finitas con palabras sobre un conjunto. Puede considerarse tambien el caso de una sucesion vacia (sin elementos), pero este caso puede escluirse dependiendo del contexto.

notacion

Existen diferentes notaciones y nociones de sucesion matematicas dependiendo del area de estudio, algunas de las cuales (como por ejemplo sucesion exacta)

Se puede utilizar la notacion (An) para indicar una sucesion en donde An hace referencia al elemento de la sucesion de la posicion n.

ejemplo:

retomando el ejemplo de los numeros positivos pares, si denotamos dicha sucesion por (Pn):

(Pn)= 2,4,6,8,10,12, ...

entonces:

P1= 2,p2 = 4, p3 = 6, p4 = 8, ...

tipos

sucesion finita: se dice que una sucesion es finita si determinamos su ultimo termino, por ejemplo el n-esimo:

Genéricamente: $a_0, \; a_1, \; a_2, \; ... \; , \; a_i , \; ... \; , \; a_n$ , donde $a_i^{}$ sería el término general si hiciese falta.

ejemplo:

100,99,98, .... , 1, 0

sucesion constante: se dice que una sucesion es constante si todos los terminos valen un mismo valor, K es decir, un mismo numero real cualquiera, ejemplo:

$a_0^{} = k, \; a_1 = k, \; a_2 = k, \; a_3 = k, \; ... \; , \; a_n = k,\;...$

ejemplo:

ejemplo: si $k_{}^{}=1$ queda como 1, 1, 1, 1, ... ,1 ,... , es decir, que todos los valores son el mismo, 1

sucesiones monotonas: una sucesion monotona es una sucesion creciente o decreciente:

sucesion creciente: Si se impone al término general de una sucesión numérica la condición que $a_n^{} < a_{n+1}$ , es decir, que el siguiente término, $a_{n+1}^{}$ , siempre sea mayor estricto que su predecesor, $a_n^{}$ , se llaman sucesiones estrictamente crecientes:

Para naturales: 1, 2, 3, 4, 5, 6, ...

Para enteros: -10, -9, -8, -7, -6, ...

Para reales: 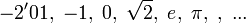$-2'01, \; -1, \; 0, \; \sqrt{2}, \; e_{}^{}, \; \pi, \; ,\;...$ .

Si se impone $a_n^{} \leq a_{n+1}$ , es decir, una desigualdad no estricta, entonces se pueden incluir, entre otras, las sucesiones constantes.

Sucesión decreciente: Al igual que las crecientes tenemos, según el término general, que:

si $a_n^{} > a_{n+1}$ es estrictamente decreciente.

si 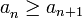$a_n^{} \geq a_{n+1}$ entonces la sucesión es decreciente.

Sucesión alternada:Intuitivamente se llama sucesión alternada cuando alterna valores de signos opuestos , como $a_n=(-1)^{n}$ que nos genera la sucesión: a₀=1, -1, 1, -1, 1, -1, ... utilizada por las series llamadas series alternadas.

Sucesiones Acotadas:Se pueden dar tres formas de sucesión acotada:

- Una sucesión {a_n} estará acotada superiormente en el caso que exista un numero real M que limite de la siguiente forma la secuencia: {a_n} ≤ M.

- Por otro lado, la sucesión estará acotada inferiormente cuando un numero real N la limite de la forma contraria a la anterior: {a_n} ≥ N.

- Finalmente, en caso de que se den ambas opciones {a_n} será una sucesión acotada.

Sucesiones Convergentes:Una sucesión $\{a_n\}, \ a_n \in \mathbb{R}$ , converge a $a$ o tiene por límite $a$ (cuando $n \rightarrow \infty$ ), y se escribe,

$\lim_{n} a_n = a$

cuando,

$\forall \epsilon \in \mathbb{R}, \epsilon > 0, \exists n_0 \in \mathbb{N} : |a_n - a| < \epsilon, \forall n \geq n_0, n \in \mathbb{N}$

Propiedades

Unicidad del límite de una sucesión

Si una sucesión $\{a_n\}, \ a_n \in \mathbb{R}$ converge, entonces el $\lim_{n} a_n$ es único.

Una sucesión $a_{1}, a_{2},...,a_{n},...$ es una sucesión aritmética si hay un número real $d$ tal que para todo entero positivo $k$ ,

$a_{k+1}=a_{k}+d$ .

El número $d=a_{k+1}-a_{k}$ se le llama diferencial común de la sucesión.

Dada una sucesion aritmetica:

$a$ k+1 = a $k$ + d

para todo entero positivo K. Esto nos da una formula recursiva para encontrar terminos sucesivos .A partir de cualquier numero real a1. obtendremos una sucesion aritmetica con diferencia comun d con solo agregar d a a1, luego a a1+d y asi sucesivamente, con lo que resulta

Observa que la diferencia común $d$ es la diferencia de dos términos sucesivos cualesquiera de una sucesión aritmética.

El n-ésimo término de una sucesión aritmética

$a_{n}=a_{n-1}+(n-1)d$

Teorema: fórmulas para $S_{n}$

Si $a_{1}, a_{2}, a_{3},...,a_{n},...$ es una sucesión aritmética con diferencia común $d$ , entonces la n-ésima suma parcial $S_{n}$ (esto es, la suma de los primeros $n$ términos), está dada por

$S_{n}=\frac{n}{2}[2a_{1}+(n-1)d]$ o $S_{n}=\frac{n}{2}(a_{1}+a_{2})$

Sucesiones Geométricas

Definición de sucesión geométrica

Una sucesión $a_{1}, a_{2},..., a_{n},...$ es una sucesión geométrica si $a_{1} \neq 0$ y si hay un número real $r \neq 0$ tal que para todo entero positivo $k$ ,

$a_{k+1} = a_{k}.r.$ .

El número $r = \frac{a_{k+1}}{a_{k}}$ se conoce la razón común de la sucesión.

Observa que la razón común $r = \frac{a_{k+1}}{a_{k}}$ es la razón entre dos términos sucesivos cualesquiera de una sucesión geométrica.

Formula para hallar el n-ésimo término de una sucesión geométrica

$a_{n}=a_{1}.r^{n-1}$ .

Teorema: fórmula para hallar $S_{n}$

La n-ésima suma parcial $S_{n}$ de una sucesión geométrica con primer término $a_{1}$ y razón común $r \neq 1 es$

$S_{n} = a_{1} \frac {1-r^n}{1-r}$ .

progresiones aritmeticas

Las Progresiones Aritméticas son sucesiones en las que cada término se obtiene sumando una misma cantidad d -que puede ser positiva o negativa- al término anterior. Es decir: a_n=a_n-1+d. La cantidad d que se va sumando se llama diferencia. Las sucesiones a_n y b_n de los ejercicios anteriores son progresiones aritméticas de diferencias d=3 y d=-40 respectivamente.

Conociendo el primer término a₁ y la diferencia de una progresión aritmética se calcula el término general de la sucesión por la siguiente fórmula:

También es posible hallar la suma de los n primeros términos de una progresión aritmética. Para ello utilizamos la fórmula

progresiones geometricas

Las Progresiones Geométricas son sucesiones en las que cada término se obtiene multiplicando por una misma cantidad r -que puede ser positiva o negativa- al término anterior. Es decir: a_n=a_n-1.r. La cantidad r por la que se va multiplicando se llama razón. Las sucesiones c_n y e_n de los ejercicios anteriores son progresiones geométricas de razón d=0'5 y d=10 respectivamente.

Conociendo el primer término s₁ y la razón de una progresión geométrica se calcula el término general de la sucesión por la siguiente fórmula:

También es posible hallar la suma de los n primeros términos de una progresión geométrica. Para ello utilizamos la fórmula:

Volver

sucesión matematica

Contacto